Kanjis, Clusters, and Gelb's Hypothesis

Paper

I'm still working on this page, but our paper is here. I (Daan van den Berg) welcome all feedback you might have. Look me up in the UvA-directory, on LinkedIn or FaceBook.

Japanese Kanji Characters

The whole idea was quite simple actually, and born from the language enthousiasm of three programmers. Not an easy language of choice, Japanese sports an approximately 60,000-piece character set named Kanji. You only need to learn about 2,000 though to read Japanese, and as a serious study also involves writing, this proved a formidable exercise. But there is some systemacity; many Kanji consist of one or more components, which are a only 252 in number. Individual Kanji are said to carry meaning in a word-like manner, and akin to how compound words are built up ("swordfish", "snowball", "wonderland"), kanji often derive meaning from their combined constituent components, and are thus explained as such in textbooks for Japanese children. But the process of learning Japanese as a Dutch grown up is quite different from Japanese children. Some of the "combined-component-meaning just seemed unlogical. As programmers we playfully drew out some networks, connecting two characters if they shared one or more components. But as we found access to electronic dictionary files containing all Kanji and their constituent components we could analyze the language network as a whole. The results were quite surprising, and actually turned out to fit in quite nicely with the exisiting scientific literature of language networks.

Some Japanese Kanji characters. The bottom-left character and its right hand neighbour can be seen sharing the tree-component.

Kanjis & Small-Worlds

The network of connected Kanji turned out to be a small-world network, which means it has a high clustering coefficient, a low average path length and a low connection density. As we found out soon enough, computational linguists had already found a large number of small-worlds on various levels in different languages, but this network of Kanji sharing components was not ye one of them. As such, it neatly lined up with existing research in quantitative linguistics and was accepted as a valuable addition. Small-worlds are also found in brains, social networks, software architecture and power grids. This is remarkable, because randomly wiring up a network almost never leads to small-worlds. So why do all these these networks share these characteristics? Maybe because they are subject to the same forces of formation. Some experimental models show that by synchronizing activity between artificial neurons, networks tends to build clusters and shortcuts in networks - by themselves. This kind of behaviour is called self-organization, and the resulting properties are sometimes referred to as emergent. But why do brains and languages self-organize to similar structures? Could it be that communication between humans is in some very basic way similar to communication between brain cells?

The functional connectivity graph of the brain is one of many well known small-worlds See Sporns & Honey (2006) and others. Image adapted from Sporns' book "Discovering the Human Connectome"

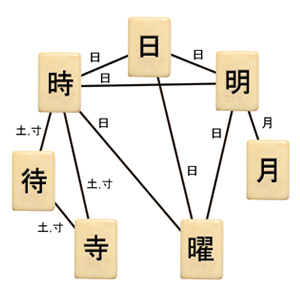Kanji characters, when connected by shared components (labels on edges) form a small-world network.

Clustering Coefficient & Average Path Length (optional)

First let's have a brief look at what makes a small-world network a small-world network, it's not all that difficult. First of all: it's about sparse networks, that is, networks with relatively low edge densities. Small-World networks have a high clustering coefficient. The clustering coefficient on a vertex is the fraction of connections between its neighbours. Vertex C has four neighbours. Between these four we have three edges, out of a possible six, so the clustering coefficient on C is 0.5. Similarly, the clustering coefficient on B is 1, and on F it is 0.33 if we disregard the two neighbours it must have outside the picture. If we don't disregard those, it has five neighbours with either one or two connections between them, so the clustering coefficient on F would be either 0.1 or 0.2. The cluster coefficient of the network is simply the average of all its vertices. The term "small-world" was originally associated with global connectivity of a graph, often cojoined by the metaphor of "six degrees of separation". For scientific quantification however, we need a more precise definition which is the average path length (shortest distance) between two vertices in a graph. In this graph, the path length from B to E is three, the path length from C to G is 2 and the path length from C to D is 1. The average path length is the average of all path lengths between vertice pairs. A small-world network has a low average path length. It's easy to see now why the term 'small-world network' is usually associated with sparse graphs, because the denser the graph, the higher the Clustering Coefficient and the lower the Average Path Length. In fact, for very dense graphs, it's impossible 'not' to have a small-world.

onderschriftonderschriftonderschriftonderschriftonderschriftonderschriftonderschriftonderschriftonderschriftonderschriftonderschrift

Gelb's Hypothesis: from pictures to sounds

So many language networks have small-world properties. But for Japanese, there's a little more to it. Because as it turns out, there's an old conjecture by Igancy Jay Gelb (1907-1985) and it appears to coincide with our findings quite neatly. An American linguist from Polish descent, Gelb hypothesized that all written languages go through a phase transition from being picture-based to being sound-based. Studied deeply, this idea is quite coarse and the exact trajectory might differ from language to language, but the core concept remains quite alluring, especially where it concerns Japanese Kanji. Although many textbooks claim 'compound meanings' for Kanji characters, a few studies have been conducted to components corresponding to sounds rather than to meaning. In fact, a few convincing examples exist of Kanji that share a component, and a pronunciation, but not a meaning - at least not in our convincion. But what's more, an ancient character dictionary named Shouwen Jiezi, containing XXXX Kanji, adopts a YYYY-piece component index. This shows that the number of components has dropped through time. Possibly by deletion, possibly by merger, possibly by replacement but these reducing operations could account for the correspondence in components and pronunciation on the one hand, and discorrespondence in meaning on the other.

Ignace Jay Gelb (1907-1985), and his hypothesis as visualized by Tadao Miyamoto in his 2007-paper. Note how these initially quite pictorial characters in this Cuneiform script evolve to a set of characters built up from relatively repetitive components.

Kanjis correspond to sounds too

So it seems that succesive disappearance of visual features accounts for the clustering found in the network of Kanji. In other words: Kanji have become simpler through time. They are nowhere near the elaborate pictures they were around 2,000 years ago, but in many ways symbolic abstractions of their ancient precursors. In the mean time, there is some evidence that certain components imply pronounciation. For instance: many of the characters containing the 'middle'-component have a pronunciation "chuu", and many Kanji with the 'orders'-component have a pronunciation 'rei'. Yet, many of these Kanji seem a world apart when it comes to their meaning. Why do the Kanji for mushroom, wise, bell and actor all have an order-component? Is there really a shared meaning in these characters? Or is it imaginable that through

Kanji evolution through time. Notice how visual similarity has increased, especially between 'horse' and 'fish'. Adapted from www.tofugu.com

All these kanji have the pronunciation 'rei'.

Whoswho&where

Sil Westerveld (top left) is currently a programmer voor SuperSAAS but did a lot ground work for the analysis together with Mark. He programmed the algorithms and gathered the data. He was also resposinble for visualizing the networks. Sil sepaks, reads and writes Japanese. Sandjai Bhulai (top right) is full professor Data Analytics and Business Intelligence at VU University in Amsterdam. He helped write, correct and finalize the paper for publication at the 2017 IARIA Data Analytics Conference in Barcelona. Mark Jeronimus (naka) built up the first algorithms and analysis of Cluster Coefficient and Average Path Length calculations in the character network. He currently works as a programmer for AirSupplies BV and is a Japanese language enthousiast. Cees van Leeuwen (bottom left) is full professor at University of Leuven. He is an expert on self-organizing systems and small-world networks, especially when it comes to perceptual models of cognitive processing. Daan van den Berg (bottom right) currently works at University of Amsterdam as a researcher & lecturer in heuristics. He is a language enthousiast and did most of the writing of the paper.

Team Kanji.

More

Maybe later.