Contents
Introduction
Chips (or more precisely: integrated circuits) are found in your PC, MacBook, Android Phone and microwave oven where they perform a diversity of functions, ranging from timekeeping and motor control to arithmetic and logic. Basically a small plate of silicon, chips are usually designed logically and subsequentially transformed to a list of connectable gates. This list, commonly known as a net list is finally transformed into a 2-dimensional design on a silicon base.
This last step however, the physical real-world process of connecting the gates, is highly volatile. Good arrangements on the base lead to short connections, leading to faster circuits, whereas poor arrangements lead to slower circuits. It leads to no doubt that a good arrangement of logical gates and good wiring between them is of vital essence to the performance of the IC as a whole.
In this case, we will consider the wiring between the gates only
Example #1
Given netlist#1, connecting five logical gates on a grid. Gates cannot be on directly adjacent grid points because of the produced heat. They should be connected by wires in exact correspondence to the netlist. For reasons of simpicity, dates to not have a in- or output side; wires can enter or exit at any point from a gate. The wires must follow grid lines for reasons of manufacture, and can split in case a common source has different targets, but connections between different pairs of gates cannot cross.
| Netlist #1: | |
|---|---|
| A | B,C; |
| C | E; |
| D | B; |
| E | D |
| thumb Game #2 | 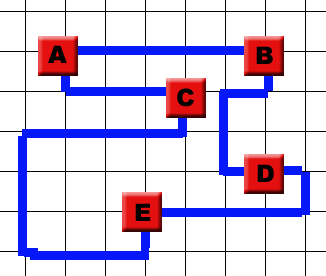
|
|---|
As can be seen, even for this one very simple netrlist, a great variety can be achieved in terms of optimality. The left picture has substantially smaller total wire length (17), resulting in a much faster processor than the right picture which is functionally identical, but a lot slower due to a much greater total wire length (32).
Assignment (part 1)
1) Write an algorithm that calculates the total wire length of any given placement of logical gates on a grid.
2) Write an algorithm that takes a netlist as input. It should check whether the wires cross, and if they do, return an error message. If the wires do not cross, it should place the gates on a grid and calculate the total wire length. It does not need to be optimal.
3) Test your algorithm on netlist #2.
4) Improve your algorithm such, that it minimizes the wire length for netlist#2. This might be quite hard.
5) Test your algorithm on netlist #3.
| Netlist #2: | |
|---|---|
| A | B,K,O,T,Q,D,H; |
| B | F,G; |
| C | T; |
| D | Q,N; |
| E | M,J,Q; |
| F | Q,H,O; |
| G | K; |
| H | Q,N; |
| I | T; |
| J | M,Q; |
| K | ; |
| L | N,Q; |
| M | Q; |
| N | P; |
| O | T; |
| P | Q; |
| Q | S,T; |
| R | ; |
| S | T; |
| T | ; |
| Netlist #3: | |
|---|---|
| A | S; |
| B | A,R; |
| C | Q; |
| D | ; |
| E | D; |
| F | A,B; |
| G | D,J; |
| H | L,M,R; |
| I | ; |
| J | D,K,I; |
| K | ; |
| L | C,D,Q; |
| M | L,R,T; |
| N | L,D,G; |
| O | H,L,N,G,K,I; |
| P | B,H,O,I; |
| Q | ; |
| R | Q; |
| S | ; |
| T | S; |
Multi-layer wire configurations
As it turns out, not every netlist can be converted into a 2D-processor design without crossing wires at least once. These problems are usually tackled by using multiple layers of wire to connected the gates as specified in the netlist. Moreover, given this new degree of freedom, it is quite possible that shorter and thus more effective arrangements can be found for existing configurations.
Assignment (part 2)
Wires can be arranged in two dimensions in one layer, but can also move up or down by a tract called a via. Moving up or down comes at the cost of one unit length. Thus, if a wire from point A to point B would have length 8 in a single-layer chip, it could also be arranged over the third layer at 4 extra cost (2 for moving down, 2 for moving up).
Advanced
The suspicion is, that the minimal number of layers required for a chip to be designed from a netlist depends on the connectivity of the netlist. Generate 10 random netlists with the exact same number of gates and connections as in netlist#3 and run them through your algorithm. Carefully document the number of layers needed and the optimality of the found solution. Next, double the number of connections for each netlist and run them through your algorithm again. Document carefully again, and compare the results with the previous experiment.
Links
Nothing here for now.
Go Back
Go back to the Heuristics Main Page.
