MeesterDaan (talk | contribs) |
MeesterDaan (talk | contribs) |
||
| Line 8: | Line 8: | ||
| − | == | + | ==Kanji? Small-World== |
<Center> | <Center> | ||
{| align="justify" | style=" align="top"; text-align:center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;" | {| align="justify" | style=" align="top"; text-align:center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;" | ||
|- | |- | ||
|valign="top"| | |valign="top"| | ||
| − | + | Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Lobortis mattis aliquam faucibus purus in. Non enim praesent elementum facilisis leo vel. Lacus vestibulum sed arcu non odio. Vivamus at augue eget arcu dictum varius duis at. Nulla facilisi morbi tempus iaculis urna id volutpat. Libero id faucibus nisl tincidunt eget nullam. At ultrices mi tempus imperdiet nulla malesuada pellentesque elit. Ac felis donec et odio pellentesque. Mollis aliquam ut porttitor leo a diam sollicitudin tempor. Sit amet nulla facilisi morbi tempus iaculis. Leo in vitae turpis massa sed elementum tempus egestas sed. Nam at lectus urna duis. Imperdiet massa tincidunt nunc pulvinar sapien et ligula. | |
| + | |||
| + | Vestibulum mattis ullamcorper velit sed ullamcorper morbi. Magna fermentum iaculis eu non diam phasellus vestibulum lorem. Ut tristique et egestas quis ipsum suspendisse. Aenean sed adipiscing diam donec. At in tellus integer feugiat scelerisque varius morbi. Massa massa ultricies mi quis. Duis at consectetur lorem donec. Ut placerat orci nulla pellentesque dignissim. Urna nunc id cursus metus aliquam. Odio euismod lacinia at quis risus sed. Convallis tellus id interdum velit laoreet. Lacinia quis vel eros donec ac odio tempor. Commodo viverra maecenas accumsan lacus vel. Nam libero justo laoreet sit amet cursus. Pellentesque massa placerat duis ultricies. Tristique sollicitudin nibh sit amet commodo. Et pharetra pharetra massa massa ultricies mi. Mollis nunc sed id semper risus. Est pellentesque elit ullamcorper dignissim cras. Faucibus purus in massa tempor nec feugiat. | ||
| + | |||
| + | Mattis molestie a iaculis at erat pellentesque adipiscing. Donec pretium vulputate sapien nec sagittis aliquam malesuada. Convallis a cras semper auctor neque vitae tempus quam pellentesque. Quisque id diam vel quam. Dui ut ornare lectus sit. Urna condimentum mattis pellentesque id nibh. Tincidunt eget nullam non nisi est sit amet. Facilisis mauris sit amet massa vitae. Cras tincidunt lobortis feugiat vivamus at augue eget. At auctor urna nunc id cursus metus aliquam. Enim blandit volutpat maecenas volutpat blandit aliquam. Auctor neque vitae tempus quam. Cras adipiscing enim eu turpis egestas pretium. Odio pellentesque diam volutpat commodo sed. Pharetra sit amet aliquam id diam maecenas ultricies mi. Quisque id diam vel quam elementum pulvinar. Parturient montes nascetur ridiculus mus. Mattis pellentesque id nibh tortor id aliquet lectus proin. Dui id ornare arcu odio ut sem nulla pharetra. | ||
| − | |||
| Line 31: | Line 34: | ||
|valign="top"| | |valign="top"| | ||
| − | + | Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Lobortis mattis aliquam faucibus purus in. Non enim praesent elementum facilisis leo vel. Lacus vestibulum sed arcu non odio. Vivamus at augue eget arcu dictum varius duis at. Nulla facilisi morbi tempus iaculis urna id volutpat. Libero id faucibus nisl tincidunt eget nullam. At ultrices mi tempus imperdiet nulla malesuada pellentesque elit. Ac felis donec et odio pellentesque. Mollis aliquam ut porttitor leo a diam sollicitudin tempor. Sit amet nulla facilisi morbi tempus iaculis. Leo in vitae turpis massa sed elementum tempus egestas sed. Nam at lectus urna duis. Imperdiet massa tincidunt nunc pulvinar sapien et ligula. | |
| + | |||
| + | Vestibulum mattis ullamcorper velit sed ullamcorper morbi. Magna fermentum iaculis eu non diam phasellus vestibulum lorem. Ut tristique et egestas quis ipsum suspendisse. Aenean sed adipiscing diam donec. At in tellus integer feugiat scelerisque varius morbi. Massa massa ultricies mi quis. Duis at consectetur lorem donec. Ut placerat orci nulla pellentesque dignissim. Urna nunc id cursus metus aliquam. Odio euismod lacinia at quis risus sed. Convallis tellus id interdum velit laoreet. Lacinia quis vel eros donec ac odio tempor. Commodo viverra maecenas accumsan lacus vel. Nam libero justo laoreet sit amet cursus. Pellentesque massa placerat duis ultricies. Tristique sollicitudin nibh sit amet commodo. Et pharetra pharetra massa massa ultricies mi. Mollis nunc sed id semper risus. Est pellentesque elit ullamcorper dignissim cras. Faucibus purus in massa tempor nec feugiat. | ||
| + | |||
| + | Mattis molestie a iaculis at erat pellentesque adipiscing. Donec pretium vulputate sapien nec sagittis aliquam malesuada. Convallis a cras semper auctor neque vitae tempus quam pellentesque. Quisque id diam vel quam. Dui ut ornare lectus sit. Urna condimentum mattis pellentesque id nibh. Tincidunt eget nullam non nisi est sit amet. Facilisis mauris sit amet massa vitae. Cras tincidunt lobortis feugiat vivamus at augue eget. At auctor urna nunc id cursus metus aliquam. Enim blandit volutpat maecenas volutpat blandit aliquam. Auctor neque vitae tempus quam. Cras adipiscing enim eu turpis egestas pretium. Odio pellentesque diam volutpat commodo sed. Pharetra sit amet aliquam id diam maecenas ultricies mi. Quisque id diam vel quam elementum pulvinar. Parturient montes nascetur ridiculus mus. Mattis pellentesque id nibh tortor id aliquet lectus proin. Dui id ornare arcu odio ut sem nulla pharetra. | ||
| − | |||
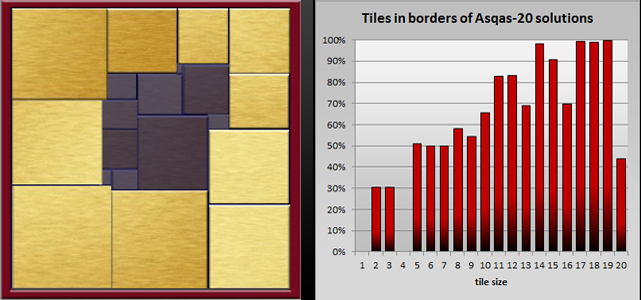
|valign="top" |[[Image:ASQAS20heur.jpg|frame|link=Heuristieken|Most of ASQAS-20 solutions have large border tiles. In fact, tiles 14x15, 17x18, 18x19, 19x20 are in the border of nearly all 54,992 solutions.]] | |valign="top" |[[Image:ASQAS20heur.jpg|frame|link=Heuristieken|Most of ASQAS-20 solutions have large border tiles. In fact, tiles 14x15, 17x18, 18x19, 19x20 are in the border of nearly all 54,992 solutions.]] | ||
Revision as of 21:21, 9 December 2017
- This page is a stub. Our paper will be obtainable via this site after publication.
Contents
Paper
I'm still working on this page, but our paper is here. I (Daan van den Berg) welcome all feedback you might have. Look me up in the UvA-directory, on LinkedIn or FaceBook.
Kanji? Small-World
|
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Lobortis mattis aliquam faucibus purus in. Non enim praesent elementum facilisis leo vel. Lacus vestibulum sed arcu non odio. Vivamus at augue eget arcu dictum varius duis at. Nulla facilisi morbi tempus iaculis urna id volutpat. Libero id faucibus nisl tincidunt eget nullam. At ultrices mi tempus imperdiet nulla malesuada pellentesque elit. Ac felis donec et odio pellentesque. Mollis aliquam ut porttitor leo a diam sollicitudin tempor. Sit amet nulla facilisi morbi tempus iaculis. Leo in vitae turpis massa sed elementum tempus egestas sed. Nam at lectus urna duis. Imperdiet massa tincidunt nunc pulvinar sapien et ligula. Vestibulum mattis ullamcorper velit sed ullamcorper morbi. Magna fermentum iaculis eu non diam phasellus vestibulum lorem. Ut tristique et egestas quis ipsum suspendisse. Aenean sed adipiscing diam donec. At in tellus integer feugiat scelerisque varius morbi. Massa massa ultricies mi quis. Duis at consectetur lorem donec. Ut placerat orci nulla pellentesque dignissim. Urna nunc id cursus metus aliquam. Odio euismod lacinia at quis risus sed. Convallis tellus id interdum velit laoreet. Lacinia quis vel eros donec ac odio tempor. Commodo viverra maecenas accumsan lacus vel. Nam libero justo laoreet sit amet cursus. Pellentesque massa placerat duis ultricies. Tristique sollicitudin nibh sit amet commodo. Et pharetra pharetra massa massa ultricies mi. Mollis nunc sed id semper risus. Est pellentesque elit ullamcorper dignissim cras. Faucibus purus in massa tempor nec feugiat. Mattis molestie a iaculis at erat pellentesque adipiscing. Donec pretium vulputate sapien nec sagittis aliquam malesuada. Convallis a cras semper auctor neque vitae tempus quam pellentesque. Quisque id diam vel quam. Dui ut ornare lectus sit. Urna condimentum mattis pellentesque id nibh. Tincidunt eget nullam non nisi est sit amet. Facilisis mauris sit amet massa vitae. Cras tincidunt lobortis feugiat vivamus at augue eget. At auctor urna nunc id cursus metus aliquam. Enim blandit volutpat maecenas volutpat blandit aliquam. Auctor neque vitae tempus quam. Cras adipiscing enim eu turpis egestas pretium. Odio pellentesque diam volutpat commodo sed. Pharetra sit amet aliquam id diam maecenas ultricies mi. Quisque id diam vel quam elementum pulvinar. Parturient montes nascetur ridiculus mus. Mattis pellentesque id nibh tortor id aliquet lectus proin. Dui id ornare arcu odio ut sem nulla pharetra.
|
How did you solve it?
|
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Lobortis mattis aliquam faucibus purus in. Non enim praesent elementum facilisis leo vel. Lacus vestibulum sed arcu non odio. Vivamus at augue eget arcu dictum varius duis at. Nulla facilisi morbi tempus iaculis urna id volutpat. Libero id faucibus nisl tincidunt eget nullam. At ultrices mi tempus imperdiet nulla malesuada pellentesque elit. Ac felis donec et odio pellentesque. Mollis aliquam ut porttitor leo a diam sollicitudin tempor. Sit amet nulla facilisi morbi tempus iaculis. Leo in vitae turpis massa sed elementum tempus egestas sed. Nam at lectus urna duis. Imperdiet massa tincidunt nunc pulvinar sapien et ligula. Vestibulum mattis ullamcorper velit sed ullamcorper morbi. Magna fermentum iaculis eu non diam phasellus vestibulum lorem. Ut tristique et egestas quis ipsum suspendisse. Aenean sed adipiscing diam donec. At in tellus integer feugiat scelerisque varius morbi. Massa massa ultricies mi quis. Duis at consectetur lorem donec. Ut placerat orci nulla pellentesque dignissim. Urna nunc id cursus metus aliquam. Odio euismod lacinia at quis risus sed. Convallis tellus id interdum velit laoreet. Lacinia quis vel eros donec ac odio tempor. Commodo viverra maecenas accumsan lacus vel. Nam libero justo laoreet sit amet cursus. Pellentesque massa placerat duis ultricies. Tristique sollicitudin nibh sit amet commodo. Et pharetra pharetra massa massa ultricies mi. Mollis nunc sed id semper risus. Est pellentesque elit ullamcorper dignissim cras. Faucibus purus in massa tempor nec feugiat. Mattis molestie a iaculis at erat pellentesque adipiscing. Donec pretium vulputate sapien nec sagittis aliquam malesuada. Convallis a cras semper auctor neque vitae tempus quam pellentesque. Quisque id diam vel quam. Dui ut ornare lectus sit. Urna condimentum mattis pellentesque id nibh. Tincidunt eget nullam non nisi est sit amet. Facilisis mauris sit amet massa vitae. Cras tincidunt lobortis feugiat vivamus at augue eget. At auctor urna nunc id cursus metus aliquam. Enim blandit volutpat maecenas volutpat blandit aliquam. Auctor neque vitae tempus quam. Cras adipiscing enim eu turpis egestas pretium. Odio pellentesque diam volutpat commodo sed. Pharetra sit amet aliquam id diam maecenas ultricies mi. Quisque id diam vel quam elementum pulvinar. Parturient montes nascetur ridiculus mus. Mattis pellentesque id nibh tortor id aliquet lectus proin. Dui id ornare arcu odio ut sem nulla pharetra.
|
How did you solve the 4,4 million borders?
|
So then we needed to fill up the 4,4 million borders with their of 22 tiles. Combinatorially speaking, even just one puzzle of 22 tiles is too difficult to solve on a single computer, leaving us with a serious challenge. To tackle this we programmed an 'interior solver' - a small, efficient computer program capable of puzzling the 22 remaining tiles inside the borders. We ran several dozen instances of this solver on scientific supercomputers throughout The Netherlands, and set up a central server to distribute the borders, in batches of 1,000 over the supercomputers.
|
So, is this a hard problem?
|
That's a very difficult question. I don't know. It took us 55 full-time calculation days on 1,000 computer cores to find only 15 solutions, and we think we had a pretty clever approach. But then there's Giovanni Resta, an Italian guy who solved the exact same problem on his desktop computer. So is Resta brilliant, or just lucky? Probably a little bit of both. Or maybe the problem isn't so hard after all. But if it wasn't that hard, why did it take us 80,000 computer days? I just don't know, to be honest.
|
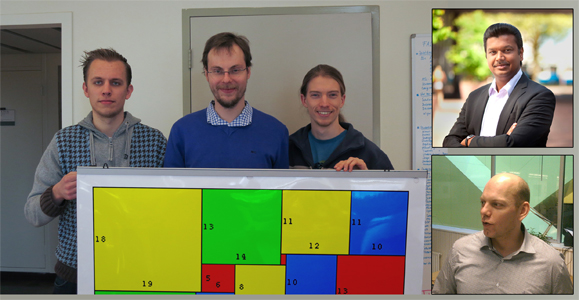
 Left: solution found on the server of Cees van Leeuwen's [lab for perceptual dynamics] in Leuven. Thanks to Marco Maas for helping out too. Right: solution found on the astronomical supercomputer ASTRON in Dwingeloo, The Netherlands |
Who are you guys?
|
We are a genuine VU-UvA consortium. Mark, Florian and Emiel were VU-students when we started this work. They're all professionals now, and Emiel does some occasional work in proofreading Heuristics-reports at the UvA. That's where I work, in the minor programming where we teach the course of Heuristics. That course was originally built up at the VU back when I worked there with Guszti Eiben and Bushra Malik. Sandjai, our senior author, also works at the VU as a Full Professor Business Analytics. He works on state-space reductions which is exactly the trick we deployed to solve ASQAS-34. So there's connections all over, we're truly a VU-UvA team. |