De Glasmeesters

Case: De Glassneyders Naar een suggestie van Misha Paauw.

a) Orderlist 1 in zo min mogelijk platen, Orderlist 2 in zo min mogelijk platen b) titoe c) Drie orderlists, veiligheidsglas (andere dim), kogelwerend glas (weer andere dim) d) Driehoekjes Advanced e) Maak een aantal random orderlists. Welke kun je makkelijk / moeilijk met weinig redundantie

Inleiding

"De Glasmeesters" is een bedrijf dat gebroken glazen in woonhuizen vervangt. Het heeft een eigen fabriek, die glasplaten van 5 bij 8 meter produceert. Eén per twee uur, maar de fabriek draait wel 24 uur door omdat het onderbreken van het smeltproces en heropstarten van de oven twee dagen vol vermogen kost. Die glasplaten zijn dus duur, en het is zaak dat de snijderij zoveel mogelijk ruiten uit zo min mogelijk glasplaten snijdt, en de waste zo klein mogelijk houdt.

Opdracht

De snijderij dus een ruime voorraad van glasplaten staan. Er is een order van een Rotterdamse woningcorporatie binnengekomen. Ze willen in één keer x ruiten van verschillende huizen, galerijwoningen en appartement vervangen.

a) Zorg ervoor dat de order van corporatie uit zo min mogelijk platen gesneden wordt.

b) In navolging van Rotterdam hebben drie Brabantse coroporaties ook een order geplaatst. Zorg dat deze drie orders ook uit zo min mogelijk platen gesneden worden.

De Glasmeesters produceert naast het standaard dubbelglas (type I) ook versterkt glas (Type II) en dubbel versterkt glas (Type III). Glas van type II wordt onder meer gebruikt in hoge torenflats vanwege de krachtige wind, en komt in platen van 5 bij 7 meter. Type III vind je in zwembaden, gymzalen, politiebureaus en luchthavens. Het is vanwege de hoge slagbestendigheid wat moeilijker te produceren en komt in platen van 4,5 bij 6 meter.

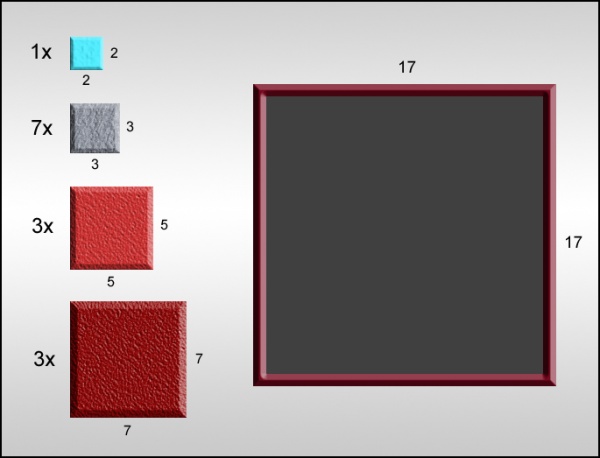
a) Verzin een algoritme om tegelset #1 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen.

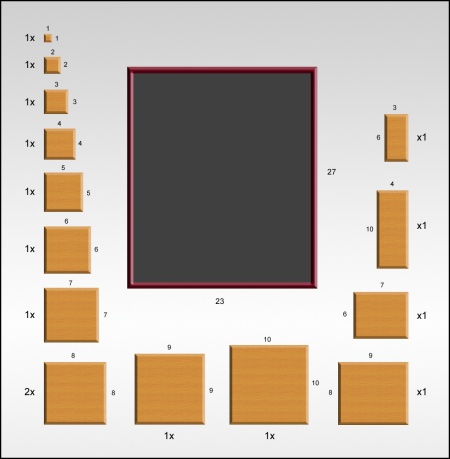
b) Verzin een algoritme om tegelset #2 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen. Tegels hoeven niet gedraaid te worden.

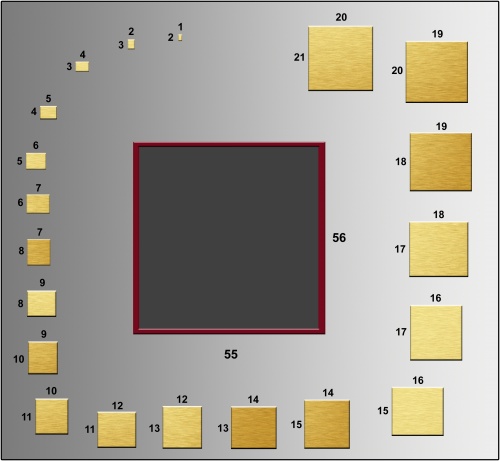
c) Verzin een algoritme om tegelset #3 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen.

Tegelset #1	Tegelset #2	Tegelset #3

Advanced

d) Er zijn nieuwe tegelsets beschikbaar gemaakt door onze collega's van de VU, maar zijn ze eigenlijk wel oplosbaar?

e) En ook de docent doet een duit in het zakje met 14 nieuwe tegelsets. Ook hiervan weten we niet of ze wel een oplossing hebben. Spannend.

Links

Best leuk om even te kijken naar perfect squares op WolframMathWorld.

Terug

Terug naar de Heuristieken hoofdpagina.