|
|
| Line 57: |
Line 57: |
| | </Center> | | </Center> |
| | | | |
| − | ==Gelb's Hypothesis: from pictures to sounds== | + | ==Gelb's Hypothesis: from Pictures to Sounds== |
| | <Center> | | <Center> |
| | {| align="justify" | style=" align="top"; text-align: center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;" | | {| align="justify" | style=" align="top"; text-align: center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;" |
Revision as of 23:11, 25 February 2018
Paper
I'm still working on this page, but our paper is here. I (Daan van den Berg) welcome all feedback you might have. Look me up in the UvA-directory, on LinkedIn or FaceBook.
Japanese Kanji Characters
|
The whole idea was quite simple actually, born from the language enthousiasm of three programmers. But Japanese is not an easy language of choice, as it features a 60,000-piece character set named Kanji. Although you 'only' need to learn about 2,000 to read the language, this is still a formidable exercise in itself. There is some systematicity though, as many Kanji are composed of one or more of 252 components, and some combinations are more common tha others. Individual Kanji-characters are said to carry meaning in a word-like manner, and akin to how compound words are built up ("swordfish", "snowball", "fireplace"), kanji often derive meaning from the combination of components, and are thus often explained as such in textbooks for Japanese children and foreign students of the language.
But the process of Japanese language aquisition is quite different for Dutch adults than for Japanese children. Adult language learners do not easily take things for granted, have trouble accepting things "as they are", and are more aware of the (in)consistencies they encounter when studying a language. We, as programmers, tried to 'understand the system' of written Japanese, drawing out networks, connecting two characters if they shared one or more components. One thing led to another, and as we got access to electronic dictionary files listing all Kanji and their constituent components, we could eventually analyze the connected-Kanji-network as a whole. The results were quite surprising, and actually turned out to fit in quite nicely with the existing scientific literature of language networks.
|
 Some Japanese Kanji characters. The bottom-left character and its right hand neighbour can be seen sharing the tree-component. |
Kanjis & Small-Worlds
|
The network of connected Kanji turned out to be a small-world network, which means it has a high clustering coefficient, a low average path length and a low connection density. At the time, computational linguists had already found a large number of small-world networks in different languages on various levels, but this network of Kanji sharing components was not yet one of them.
Remarkably enough, small-world networks are also found in networks of connected brain cells, social relationships, software architecture and power grids. This is somewhat counterintuitive, because randomly wiring up a network almost never leads to a small-world network. So why do all these these networks share these characteristics if their likelihood of existence is so small? Maybe because they are subject to the same forces of formation. Some experimental models for artificial brains tend to build clusters and shortcuts while synchronizing neuronal activity. As these systems do not have an architect for their topology, they arrange into small-world topologies completely by themselves. This kind of behaviour is called self-organization, and the resulting properties are sometimes referred to as emergent. But why would brains and languages self-organize to similar structures? Could it be that communication between two humans is in some very basic way similar to communication between two brain cells?
|
 The functional connectivity graph of the brain is one of many well known small-worlds See Sporns & Honey (2006) and others. Image adapted from Sporns' book "Discovering the Human Connectome" |
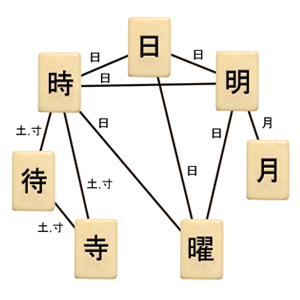 Kanji characters, when connected by shared components (labels on edges) form a small-world network. |
Clustering Coefficient & Average Path Length (optional)
|
First let's have a brief look at what makes a small-world network a small-world network. First of all: small-world networks are sparse networks, that is, networks with relatively few edges. Second, small-world networks have a high clustering coefficient. The clustering coefficient on a vertex is the fraction of edges between its neighbours. As an example, look at the figure. Vertex C has four neighbours and between these four we have three edges, out of a possible six, so the clustering coefficient on C is 0.5. Similarly, the clustering coefficient on B is 1, and on F it is 0.33 if we disregard the two neighbours it must have outside the figue. If we don't disregard those, it has five neighbours with either one or two connections between them, so the clustering coefficient on F would be either 0.1 or 0.2. The cluster coefficient of the network is simply the average of all its vertices.
The term "small-world" was originally associated with global connectivity of a graph, often accompanied by the metaphor of "six degrees of separation". For scientific quantification however, we need a more precise definition. The average path length (APL) of a graph is the averaged shortest distance between two vertices in a graph. In this graph, the path length from B to E is three, the path length from C to G is 2 and the path length from C to D is 1. The average path length is the average of all path lengths between vertice pairs. A small-world network has a low average path length, being its third defining characteristic after sparseness and high clustering coefficient.
It's now easy to see why the term 'small-world network' is usually associated with sparse graphs. The denser the graph, the higher the Clustering Coefficient and the lower the Average Path Length. In fact, for very dense graphs, it's impossible 'not' to have a small-world.
|
 The four neighbours of vertex C have three edges between them, out of a possible six. Therefore, the CC on C is 0.5. To get from C to G, you must traverse a minimum of 2 edges, so the path length from C to G is 2. |
Gelb's Hypothesis: from Pictures to Sounds
|
Many language networks have small-world properties but for Japanese Kanji, there's a little more to it. An old conjecture by Ignacy Jay Gelb (1907-1985), states that all written languages go through a phase transition from being picture-based to being sound-based. The idea original is quite coarse and the exact trajectory might differ from language to language, but the conjecture is alluring where it concerns clustering in Japanese Kanji.
Kanji characters are often explained as symbols of 'compound meaning', built up from individual meaningful components. But these explanations seem anecdotical rather than scientific. For Kanji characters, some studies have related components to sounds rather than to meaning. In fact, a few convincing examples exist of Kanji that share a component, and a pronunciation, but not a meaning. But what's more, an ancient character dictionary named Shuowen Jiezı, containing 9353 Kanji, adopts a 540-piece component index. This shows that the number of components must have dropped through time by deletion, by merger, transformtation or by replacement of individual components.
These reduction operations could account for the correspondence in components and pronunciation on the one hand, and discorrespondence in meaning on the other, as such being the driving mechanism behind the Gelbian Phase Transition.
|
 Ignace Jay Gelb (1907-1985), and his hypothesis as visualized by Tadao Miyamoto in his 2007-paper. Note how these initially quite pictorial characters in this Cuneiform script evolve to a set of characters built up from relatively repetitive components. |
Kanjis & Clusters: A Gelbian Phase Transition
|
So it seems that successive disappearance of visual features accounts for the clustering found in the Kanji-network. Modern-day Kanji characters are systematically structured, and nowhere near the elaborate pictures they were around 2,000 years ago.
Simultaneously, there is some evidence that some components correlate closely to a Kanji's pronounciation. Studies by Townsend (2011) and Toyoda, Fardius and Kano (2013) have yielded large sets of components that "can be used by students to guess their pronunciation". For instance: many of the characters containing the 'middle'-component have a pronunciation "chuu", and many Kanji with the 'orders'-component have a pronunciation 'rei'. Yet, many of these Kanji sharing such a 'speech-component' seem a world apart when it comes to their meaning. Why do the Kanji for mushroom, wise, bell and actor all have an orders-component? Is there really a shared meaning in these characters? Or have the components actually taken on somewhat of an alphabetic function?
We think they have, and as such regard small-worldness in Japanese Kanji characters as a byproduct of a language going through a Gelbian phase transition. Many ancient writing systems around the world began as series of pictures, but most of them have transformed to an alfabetical system over time, or have disappeared. Japanese, a rarity in linguistics, is still in the midst of this transformation, and complex network analysis provide the tools to quantify this transformation, and explain why written Japanese is as it is today.
|
 Kanji evolution through time. Notice how visual similarity has increased, especially between 'horse' and 'fish'. Adapted from www.tofugu.com |
 These seven characters all share a visual component, and a pronunciation ("rei"). Although Kanji meaning are often explained through combined components, this explanation looks unconvincing in some cases. Do components really add an element of meaning to a Kanji? Or is it actualy an element of sound? |
The Team
- Sil Westerveld (top left) is currently a programmer voor SuperSAAS but did a lot ground work for the analysis together with Mark. He programmed the algorithms and gathered the data. He was also resposinble for visualizing the networks. Sil sepaks, reads and writes Japanese.
- Sandjai Bhulai (top right) is full professor Data Analytics and Business Intelligence at VU University in Amsterdam. He helped write, correct and finalize the paper for publication at the 2017 IARIA Data Analytics Conference in Barcelona.
- Mark Jeronimus (naka) built up the first algorithms and analysis of Cluster Coefficient and Average Path Length calculations in the character network. He currently works as a programmer for AirSupplies BV and is a Japanese language enthousiast.
- Cees van Leeuwen (bottom left) is full professor at University of Leuven. He is an expert on self-organizing systems and small-world networks, especially when it comes to perceptual models of cognitive processing.
- Daan van den Berg (bottom right) currently works at University of Amsterdam as a researcher & lecturer in heuristics. He is a language enthousiast and did most of the writing of the paper.
|
 Team Kanji. |
More
Maybe later.







