MeesterDaan (talk | contribs) (Created page with " thumb|right|Een versailles-patroon. ==Inleiding== Tegelzetten is een vak apart. Hoewel de meeste zettingen regelmatig zijn (denk aan de vierk...") |
MeesterDaan (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | [[Image:numbercrunching2.jpg|thumb|right | + | [[Image:numbercrunching2.jpg|thumb|right]] |
==Inleiding== | ==Inleiding== | ||
| − | + | De basisingredienten van deze opgave zijn erg eenvoudig: het getal 4 en drie operatoren: de faculteit, de vierkantswortel en de floor-functie, in het nederlands beter bekend als 'afronden naar beneden'. Er bestaat een hypothese dat alle natuurlijke getallen met deze drie operatoren uit de vier gemaakt kunnen worden. We gaan deze hypothese testen, en hopelijk enige klein beetje vordering maken in het oplossen van dit vraagstuk. | |
| − | |||
==Opdracht== | ==Opdracht== | ||
Revision as of 18:17, 22 February 2014
Contents
Inleiding
De basisingredienten van deze opgave zijn erg eenvoudig: het getal 4 en drie operatoren: de faculteit, de vierkantswortel en de floor-functie, in het nederlands beter bekend als 'afronden naar beneden'. Er bestaat een hypothese dat alle natuurlijke getallen met deze drie operatoren uit de vier gemaakt kunnen worden. We gaan deze hypothese testen, en hopelijk enige klein beetje vordering maken in het oplossen van dit vraagstuk.
Opdracht
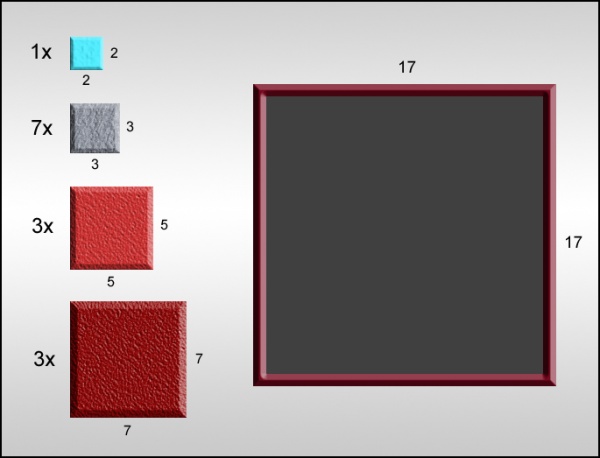
a) Verzin een algoritme om tegelset #1 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen.
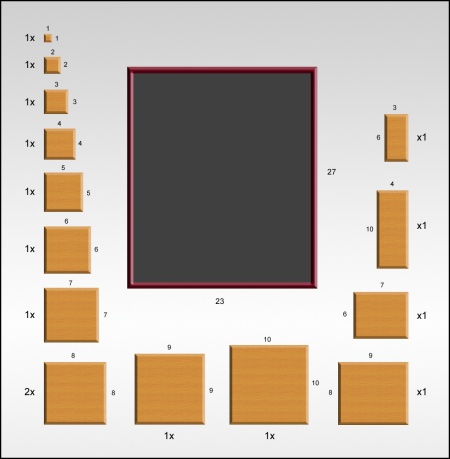
b) Verzin een algoritme om tegelset #2 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen. Tegels hoeven niet gedraaid te worden.
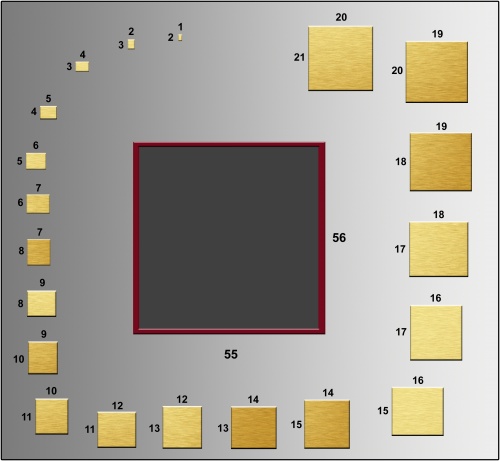
c) Verzin een algoritme om tegelset #3 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen.
Advanced
We werken met rechthoeken waarvan de ene zijde net één eenheid korter is dan de andere zijde. Deel c van de vorige opdracht bestaat uit rechthoeken 1 tot en met 20 (1x2, 2x3, 3x4 .... 20x21), die samen in een groter rechthoek (55x56) passen. Kijk of er een oplossing bestaat voor 1 tot en met 34. Je weet niet of de rechthoeken gedraaid moeten worden, en hoe groot het invoervlak moet zijn. Probeer het zo goed mogelijk te passen!
Links
Best leuk om even te kijken naar perfect squares op WolframMathWorld.
Terug
Terug naar de Heuristieken hoofdpagina.