Couveuse

Welkom in de couveuse

De couveuse is een plaats waar spontaan ontsproten ideeën voor het vak AI-course langzaam worden uitgebroed.

Programmeertalen en compilersnelheid

Deze suggestie is geleverd door Dr. Dion Gijswijt (CWI / Univ. Leiden). Het lijkt erg te raken aan formele talen (programmeertalen), berekenbaarheid een compilervraagstukken, zoals interpretatiesnelheid. De nog premature casus gaat als volgt:

We bekijken woorden opgebouwd uit de drie letters T, A en M. Zo’n woord mag je met behulp van de volgende spelregels veranderen:

1) Je mag een M veranderen in MT.

2) Je mag een T veranderen in TA.

3) Je mag een A veranderen in TAM.

4) Twee gelijke letters die naast elkaar staan mag je wegstrepen.

De casus:

Je hebt twee woorden, namelijk 1:MATTAMAMAT en 2:TATAMATMT.

Welke set regels verandert woord 1 in woord 2?

Welke set regels verandert woord 2 in woord 1?

Maak twee andere random woorden en vind nogmaals twee regelsets.

Opties voor tegelzetten

In de huidige vorm zijn alle sets in alle vakken een fit. Het is mogelijk te kijken naar sets die niet precies een fit zijn.

Local Traffic

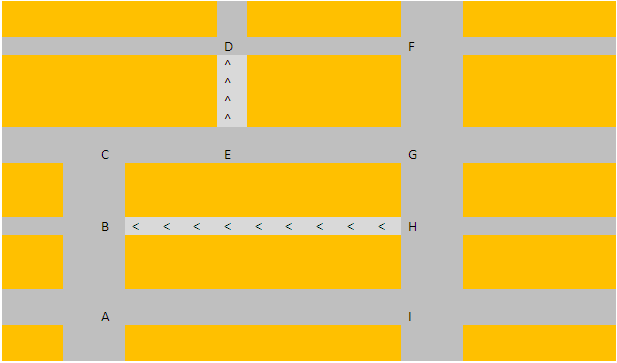
De opdracht: maak een dagschema voor de stoplichten van stadsdeel Nieuw-Noord. De kwaliteit van het dagschema is de totale wachttijd van alle auto's opgeteld dus hoe lager de score, hoe beter. Auto's komen op vaste tijden aan en rijden een vaaste route. Dit is niet erg realistisch, maar we willen graag eerst even kijken hoe de opgave uitpakt voordat we de restricties versoepelen, of stochastische complexiteit toevoegen.

• Deterministische toevoer van auto’s in de vorm van tabel 1.
• Verschillende intensiteit: ochtend- en avondspits

Wegennet van Nieuw-Noord

• Niet elk kruispunt heeft banen voor linksaf, rechtsaf en rechtdoor.
• Op een wegdeel tussen 2 kruispunten kan maar een beperkt aantal auto’s staan (?)

Wenselijk is een simulator die laat zien hoe een rooster presteert, directe score teruggeven is misschien voldoende voor een eerste-versie opgave.

Hard constraints:

• Alle auto’s moeten hun bestemming bereiken
• Stoplichten mogen niet dusdanig ingesteld staan dat ongelukken gebeuren

Nog te bepalen:

• Exacte kruispuntconfiguratie
• Auto-aankomsttijdentabel

Ziekenhuizen voor Haiti

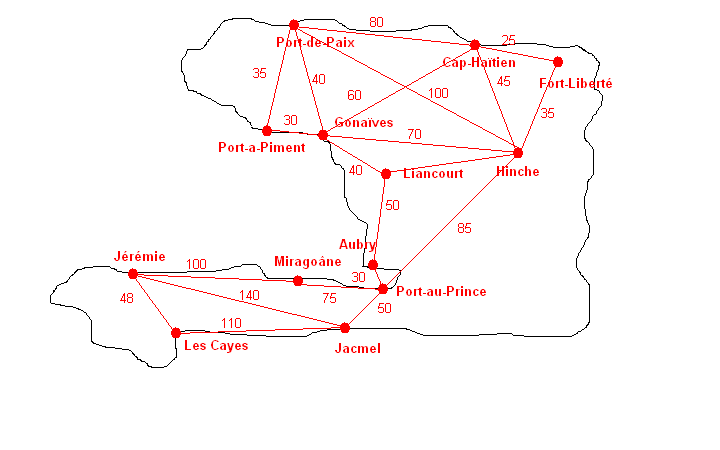
Een jaar na de zware aardbeving die het hele land in puin legde, zijn er nog steeds grote problemen in Haiti. Zo is er nog altijd nauwelijks medische hulp in het hele land. Er is echter hoop: de VN is van plan ziekenhuizen te bouwen waarmee het hele land gecoverd zal worden. De vraag is echter: welk type en waar moeten de ziekenhuizen geplaatst worden?

Opdracht

Bepaal waar, welk type ziekenhuis moet worden gebouwd, z.d.d. de kosten per geholpen patiënt zo laag mogelijk zijn.

Gegevens

Er zijn drie type ziekenhuizen die gebouwd kunnen worden, namelijk:

De type ziekenhuizen

	Prijs	Maximaal aantal patiënten per jaar	Maximale reisafstand *
Klein
Midden
Groot

Verder is ook gegeven een lijst met het inwonersaantal per stad.

Restricties A

• Je mag alleen bouwen in de steden.
• 50% van de bevolking gaat in een jaar naar een ziekenhuis.
• Elke zieke patiënt moet verzorgt worden.

Restricties B

• Je mag overal in het land bouwen.
• 50% van de bevolking gaat in een jaar naar een ziekenhuis.
• Elke zieke patiënt moet naar een ziekenhuis kunnen.

Advanced

In plaats van de deterministische “vraag” naar zorg, kan deze stochastisch worden gegenereerd a.h.v. een verdeling.

Nog te bepalen

De optimale waardes voor de tabel van de ziekenhuizen, z.d.d. de oplossing niet triviaal is. Verder kan natuurlijk ook het aantal steden nog worden uitgebreid / verminderd.

Ideeën voor Amstelhaege

• De afstand van een huis tot dichtstbijzijnde water als variabele

• Dynamische component: huizen zijn niet altijd even veel waard maar varieren binnen een bepaalde range (waarbij prijzen van maisons het meest schommelen, eengezins meer stabiel).

• Een standbeeld dat vooral veel waard is in de buurt van maisons, maar minder in de goedkopere wijken

• Een verhouding tussen wegen (waardeverbetering, maar milieuvermindering)en natuurgebied (milieuverbetering)

• Stel: Huizen hebben alleen ramen aan voor- en achterkant, en een huis wordt meer waard als er geen 'inkijk' vanuit andere huizen is.

Ideeën voor nieuwe opgaven

• Callcenter en distributie van bellers

• (Som)Sudoku-solver

• het bepalen van de moeilijkheidsgraad van een Calcudoku puzzel (voorbeeld Calcudoku's op http://www.321monkey.nl/calcudoku)

• • Gerelateerd is: hoeveel verschillende Calcudoku puzzels zijn er mogelijk, gegeven een grootte, aantal bewerkingen, en maximale "hokgrootte"? (bijv. 4x4, 2 bewerkingen, maximale hokgrootte 2)

• Supply-chain management. Verschillende machines produceren verschillende onderdelen van een auto

• 3D-traject met verschuiving en rotatie. Een bankstel in een Amsterdams trappenhuis.

• NS-uitval. Het valt op dat iedere keer als er een trein ontspoort of een wissel bevriest, de gevolgen niet beperkt blijven tot een kleine verstoring, maar vaak verstrekkende gevolgen hebben voor de dienstregeling. In ander woorden: de stabiliteit is niet heel groot. Hoe komt dat, en hoe kunnen we hier een opgave mee maken?

• Liften zo programmeren dat de gemiddelde wachttijd het kortst is.

• Zendmasten met een bepaald bereik, tegen kosten van het plaatsen.

• (Ziekenhuis) rooster voor het inboeken van personeel.

• Apotheek(voorraad) De levering van verschillende stoffen met verschillende houdbaarheden die samengesteld verschillende medicijnen vormen.

• Directieplanning; leden van bestuur moeten afhankelijk van de vergadering samen of alleen ergens aanwezig zijn.

• In het 8-queens problem moet je acht koninginnen op een schaakbord zetten zonder dat ze elkaar slaan. Hoeveel oplossingen zijn er, en hoeveel daarvan zijn er symmetrisch. Doe dit voor een 9x9, 10x10 of ander formaat schaakbord nogmaals.

• Tot nu toe zijn alle opgaven deterministisch. Kunnen we iets met een simulatie of een stochast?