From Daan
Jump to: navigation, search
m (→‎Assignment (part 1))
(→‎Questions & Answers)
 
(37 intermediate revisions by the same user not shown)
Line 3: Line 3:
  
  
−
[[Image:chipsandcircuits.jpg|thumb|right|]]
+
[[Image:chipsandcircuits2.jpg|thumb|right|]]
 +
 
 +
 
 
==Introduction==
 
==Introduction==
  
−
Chips (or more precisely: ''integrated circuits'') are found in your PC, MacBook, Android Phone and microwave oven where they perform a diversity of frunctions, ranging from timekeeping and motor control to arithmetical calculations. Basically a small plate of silicon supporting a considerable number of connected logical gates, chips are usually designed by a logical design, subsequentially transformed to a list of connectable logical gates (commonly known as a ''net list'') and in the final step transformed to 2-dimensional design on a silicon base.
+
Chips (or more precisely: ''integrated circuits'') are found in your PC, MacBook, Android Phone and microwave oven where they perform a diversity of functions, ranging from timekeeping and motor control to arithmetic and logic. Basically a small plate of silicon, chips are usually designed logically and subsequentially transformed to a list of connectable gates. This list, commonly known as a ''net list'' is finally transformed into a 2-dimensional design on a silicon base.
 +
 
 +
 
 +
This last step however, the physical real-world process of connecting the gates, is highly volatile. Good arrangements with short nets lead to faster circuits, whereas poor arrangements with long nets lead to slower circuits. Besides, shorter nets are cheaper than long nets, so there is no doubt that a good arrangement of logical gates and short nets between them is of vital importance, both economically and performancewise.
  
  
−
This last step however, the physical real-world process of connecting the gates, is highly volatile. Good arrangements on the base lead to short connections, leading to faster circuits, whereas poor arrangements lead to slower circuits. It leads to no doubt that a good arrangement of logical gates is of vital essence to the value of the IC as a whole.
+
To make things easier, we will consider the wiring problem only. The gates have already been arranged, and all it takes is finding very short wiring patterns.
  
−
==Example #1==
 
  
−
Given netlist#1, connecting five logical gates on a grid. Gates cannot be on directly adjacent grid points because of the produced heat. They should be connected by wires in exact correspondence to the netlist. For reasons of simpicity, dates to not have a  in- or output side; wires can enter or exit at any point from a gate. The wires must follow grid lines for reasons of manufacture, and can split in case a common source has different targets, but connections between different pairs of gates cannot cross.
+
==Example==
  
−
{| border="1"
+
<Center>
−
!'''Netlist #1:'''
+
{| align="center" | style=" align="center"; text-align: center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;"
−
|-
 
−
! A||B,C;
 
−
|-
 
−
! C||E;
 
 
|-
 
|-
−
! D||B;
+
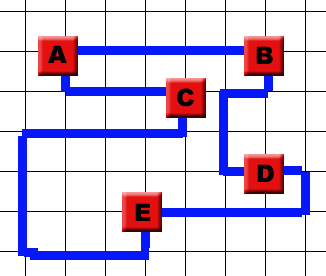
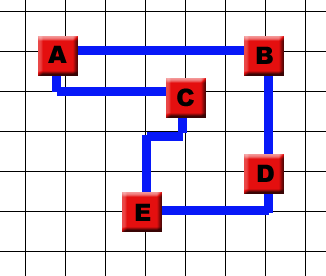
|valign="top" |[[Image:netlist1.gif|frame| Netlist #1]]
−
|-
+
|valign="top" |[[Image:cc1_subopt.gif|frame| A suboptimal wiring for netlist #1.]]
−
! E||D
+
|valign="top" |[[Image:cc1_optim.gif|frame| An optimal wiring for netlist #1.]]
 
|}
 
|}
 +
</Center>
 +
 +
 +
This is an integrated circuit built up from five gates that need to be connected. The connections ("nets") follow the grid in a Manhattan style. Luckily enough, the wires don't cross. Sometimes they have to and when they do, the base consists of multiple grid layers. Besides going North, South, East and West, nets can also go Up and Down, and the distance between levels is identical to the distance between grid points.
 +
 +
 +
==Assignment==
  
 
<Center>
 
<Center>
−
{|
+
{| align="center" | style=" align="center"; text-align: center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;"
−
![[Image:cc1_opt.gif|thumb||border|Game #2]]
+
|-
−
![[Image:cc1_subopt2.gif|thumb||border|Game #3]]
+
|valign="bottom" |[[Image:print1.gif|frame| Print #1]]
 +
|valign="bottom" |[[Image:print2.gif|frame| Print #2]]
 
|}
 
|}
 
</Center>
 
</Center>
  
 +
Print #1 and Print #2 are arrangements of gates on a base, and all it takes is to wire the appropriate gates together. There are three net lists (in [http://heuristieken.nl/resources/CC_netlists2.txt txt-format]) for each print. Each net list needs to be implemented. Nets can only follow the grid, only one wire per segment, and one step costs 1 unit length. Nets that are aligned among the same grid line are said to be in <I>collision</I>. If there is one collision in one arrangement, the circuit cannot be used. Nets can also go up and down to lower and higher layers, also at the cost of 1 per level. The assignment is to implement all nets in all netlists at minimum cost.
 +
 +
 +
A few steps to pave the way towards a program:
 +
 +
 +
1) Build a computer program that holds a data structure for a grid with fixed gates.
 +
 +
 +
2) Expand your program by making a data structure for a net list. Make sure it holds a few nets, and that the program has a cost function to calculate the total wire length.
 +
 +
 +
3) Add 7 more layers. Try to get all the nets in. You can either build up wire-by-wire, or remove collisions one by one.
  
−
As can be seen, even for this one very simple netrlist, a great variety can be achieved in terms of optimality. The left picture has substantially smaller total wire length (17), resulting in a much faster processor than the right picture which is functionally identical, but a lot slower due to a much greater total wire length (32).
 
  
−
==Assignment (part 1)==
+
4) Try to get all the nets in with minimal costs. Record all your results, so you can present them later.
  
−
1) Write an algorithm that calculates the total wire length of any given placement of logical gates on a grid.
 
  
−
2) Write an algorithm that takes a netlist as input. It should check whether the wires cross, and if they do, return an error message. If the wires do not cross, it should place the gates on a grid and calculate the total wire length. It does not need to be optimal.
+
==Advanced==
  
−
3) Test your algorithm on netlist #2.
+
* Randomly generate some new net lists. They should be of equal length to the original net lists. Which are solvable, which aren't? Which have good solutions, which haven't?
  
−
4) Improve your algorithm such, that it minimizes the wire length for netlist#2. This might be quite hard.
+
* For each of the three arrangements, try to determine the relation between the number of wires and the required number of layers.
  
−
5) Test your algorithm on netlist #3.
 
  
−
{| border="1"
+
==Questions & Answers ==
−
!'''Netlist #2:'''
+
 
−
|-
+
'''1) "only one wire per segment", does this means multiple nets can use a grid intersection?'''  
−
! A||B,K,O,T,Q,D,H;
+
 
−
|-
+
No, it doesnt. Each grid intersection can support just one net (or "wire"). Still, this might cause problems around the logical gates, so maybe an exception should be made there. We don't know yet, as this is quite a new case.
−
! B||F,G;
+
 
−
|-
+
 
−
! C||T;
+
'''2) The edges of the prints as shown in the pictures, can we use them to route nets, or should the nets stay clear of the edges?'''
−
|-
+
 
−
! D||Q,N;
+
Yes. You can consider the base to extend a little beyond the picture, and therefore all intersections in the picture can be used.
−
|-
+
 
−
! E||M,J,Q;
+
 
−
|-
+
'''3) A new layer, should it be somewhere specific, or can we place it where we want?'''
−
! F||Q,H,O,B;
+
 
−
|-
+
A new (second, third, fourth) layer provides a means for your nets to go down one extra level. A new layer is of equal dimensions as the original base. But, if a layer (for instance a seventh or eight layer) is unused, it should not be placed of course, to keep manufacturing costs down.
−
! G||B,K;
+
 
−
|-
 
−
! H||D
 
−
|-
 
−
! I||B,C;
 
−
|-
 
−
! J||E;
 
−
|-
 
−
! K||B;
 
−
|-
 
−
! L||D
 
−
|-
 
−
! M||B,C;
 
−
|-
 
−
! N||E;
 
−
|-
 
−
! O||B;
 
−
|-
 
−
! P||D
 
−
|-
 
−
! Q||B,C;
 
−
|-
 
−
! R||E;
 
−
|-
 
−
! S||B;
 
−
|-
 
−
! T||D
 
  
−
|}
+
'''4) Can unconnected gates be removed?'''
  
−
{| border="1"
+
We have updated the net lists and gate configurations. No unconnected gates exist anymore.
−
!'''Netlist #3:'''
 
−
|-
 
−
! A||B,C;
 
−
|-
 
−
! C||E;
 
−
|-
 
−
! D||B;
 
−
|-
 
−
! E||D
 
−
|}
 
  
−
==Multi-layer wires==
 
  
−
==Example #2==
+
'''5) Can nets run through gates?'''
  
−
==Assignment (part 2)==
+
No! Every net touches exactly two gates, one at both ends.
  
−
==Advanced==
 
  
−
The suspicion is, that the minimal number of layers required for a chip to be designed from a netlist depends on the connectivity of the netlist. Generate 10 random netlists with the exact same number of gates and connections as in netlist#3 and run them through your algorithm. Carefully document the number of layers needed and the optimality of the found solution. Next, double the number of connections for each netlist and run them through your algorithm again. Document carefully again, and compare the results with the previous experiment.
+
'''6) Can loose segments of several logical gates be distributed elsewhere on the base?'''
  
 +
We don't expect this situation to be present, but the answer in any case is no; gate locations are fixed.
  
 
==Links==
 
==Links==
  
−
Nothing here for now.
+
No links.
  
−
==Go Back==
+
==Bacq==
  
−
Go back to the [[Heuristieken| Heuristics Main Page]].
+
Bakc to the [[Heuristieken|Heuristics main page]].

Latest revision as of 10:15, 15 October 2018



Chipsandcircuits2.jpg


Introduction

Chips (or more precisely: integrated circuits) are found in your PC, MacBook, Android Phone and microwave oven where they perform a diversity of functions, ranging from timekeeping and motor control to arithmetic and logic. Basically a small plate of silicon, chips are usually designed logically and subsequentially transformed to a list of connectable gates. This list, commonly known as a net list is finally transformed into a 2-dimensional design on a silicon base.


This last step however, the physical real-world process of connecting the gates, is highly volatile. Good arrangements with short nets lead to faster circuits, whereas poor arrangements with long nets lead to slower circuits. Besides, shorter nets are cheaper than long nets, so there is no doubt that a good arrangement of logical gates and short nets between them is of vital importance, both economically and performancewise.


To make things easier, we will consider the wiring problem only. The gates have already been arranged, and all it takes is finding very short wiring patterns.


Example

Netlist #1
A suboptimal wiring for netlist #1.
An optimal wiring for netlist #1.


This is an integrated circuit built up from five gates that need to be connected. The connections ("nets") follow the grid in a Manhattan style. Luckily enough, the wires don't cross. Sometimes they have to and when they do, the base consists of multiple grid layers. Besides going North, South, East and West, nets can also go Up and Down, and the distance between levels is identical to the distance between grid points.


Assignment

Print #1
Print #2

Print #1 and Print #2 are arrangements of gates on a base, and all it takes is to wire the appropriate gates together. There are three net lists (in txt-format) for each print. Each net list needs to be implemented. Nets can only follow the grid, only one wire per segment, and one step costs 1 unit length. Nets that are aligned among the same grid line are said to be in collision. If there is one collision in one arrangement, the circuit cannot be used. Nets can also go up and down to lower and higher layers, also at the cost of 1 per level. The assignment is to implement all nets in all netlists at minimum cost.


A few steps to pave the way towards a program:


1) Build a computer program that holds a data structure for a grid with fixed gates.


2) Expand your program by making a data structure for a net list. Make sure it holds a few nets, and that the program has a cost function to calculate the total wire length.


3) Add 7 more layers. Try to get all the nets in. You can either build up wire-by-wire, or remove collisions one by one.


4) Try to get all the nets in with minimal costs. Record all your results, so you can present them later.


Advanced

  • Randomly generate some new net lists. They should be of equal length to the original net lists. Which are solvable, which aren't? Which have good solutions, which haven't?
  • For each of the three arrangements, try to determine the relation between the number of wires and the required number of layers.


Questions & Answers

1) "only one wire per segment", does this means multiple nets can use a grid intersection?

No, it doesnt. Each grid intersection can support just one net (or "wire"). Still, this might cause problems around the logical gates, so maybe an exception should be made there. We don't know yet, as this is quite a new case.


2) The edges of the prints as shown in the pictures, can we use them to route nets, or should the nets stay clear of the edges?

Yes. You can consider the base to extend a little beyond the picture, and therefore all intersections in the picture can be used.


3) A new layer, should it be somewhere specific, or can we place it where we want?

A new (second, third, fourth) layer provides a means for your nets to go down one extra level. A new layer is of equal dimensions as the original base. But, if a layer (for instance a seventh or eight layer) is unused, it should not be placed of course, to keep manufacturing costs down.


4) Can unconnected gates be removed?

We have updated the net lists and gate configurations. No unconnected gates exist anymore.


5) Can nets run through gates?

No! Every net touches exactly two gates, one at both ends.


6) Can loose segments of several logical gates be distributed elsewhere on the base?

We don't expect this situation to be present, but the answer in any case is no; gate locations are fixed.

Links

No links.

Bacq

Bakc to the Heuristics main page.

Retrieved from "http://heuristieken.nl/wiki/index.php?title=Chips_%26_Circuits&oldid=2587"