ASQAS-34

Paper

I'm still working on this page, but our paper is here. I (Daan van den Berg) welcome all feedback you might have. Look me up in the UvA-directory, on LinkedIn or FaceBook.

What is ASQAS-34 ?

ASQAS-34 is a Perfect Rectangle Packing Problem. In general, rectangle packing problems involve putting a set of rectangles inside a rectangular frame (often called a "container"). Those problems requires that you find the smallest container possible, hence it is an constrained optimization problem. In perfect rectangle packing problems, the frame has exactly the same area of all the rectangles summed up. This means that if it fits, it fits perfectly, without free space or overlap in the rectangles, and a smaller container does not exist. Therefore, perfect rectangle packing problems such as ASQAS-34, are constraint satisfaction problems (or equivalently: a decision problem). There are five ASQAS problems in total, and they all consist of a serie of rectangles from 1x2, 2x3, 3x4 to NxN+1 which need to be fitted into an almost-square frame. Four ASQAS problems had already been solved (ASQAS-1, ASQAS-3, ASQAS-8 and ASQAS-20). In our paper, we show that ASQAS-34 is the last instance, and that it can be solved also. This is somewhat different from consecutive squares-in-squares, which has only two instances (1 and 24), the first one being completely trivial and the second one being unsolvable.

This is Asqas-34: consecutive almost-square tiles to be fit in an almost-square frame. There are 5 instances of ASQAS, and ASQAS-34 was the only unsolved instance yet.

How did you solve it?

With 1048 possible configurations, this problem was way too big to solve on a stand-alone computer. So we needed some tricks to tip the odds in our favour. Such tricka are called "heuristics" if they involve an element of guessing, and "optimizations" if they just speed up the computation process. We pryed a valuable heuristic out of a smaller instance, the ASQAS-20. This instance had 54,992 solutions, most of which had borders consisting of large tiles. We figured that this might be true for the ASQAS-34 instance too, so we decided to first make all borders of 12 tiles and this is where we got lucky. Combinatorially speaking, we could make about 1021 of these 12-tile borders. But a single day's work showed that only 4,425,341 borders actually fitted the frame. That's less than 0.00000000001%. So that's a huge improvement, but 4,4 million borders is still a lot.

Most of ASQAS-20 solutions have large border tiles. In fact, tiles 14x15, 17x18, 18x19, 19x20 are in the border of nearly all 54,992 solutions.

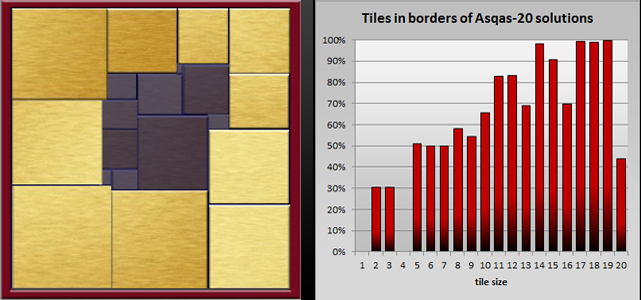
How did you solve the 4,4 million borders?

So then we needed to solve 4,4 million puzzles of 22 tiles - the interior of the borders. One puzzle of 22 tiles is too difficult to solve on one computer, so we still had a serious problem. We programmed an 'interior solver' - a small, efficient computer program capable of puzzling the 22 remaining tiles inside the borders. We put multiple copies of this program on scientific supercomputers throughout The Netherlands, and set up a central server to distribute the borders, in batches of 1,000 over the supercomputers.

A distributed approach: All 12-tiles borders were constructed first, then put in files, and then distributedly solved by 'supercomputers' around the country. It took 80 days on 1,000 computers to find all 15 solutions with 12-tile borders.

So, is this a hard problem?

That's a very difficult question. I don't know. It took us 80 full-time calculation days on 1,000 computers, and we think we used a pretty clever approach. But then there's [Giovanni Resta], an Italian guy who solved the exact same problem on his desktop computer. So is Resta brilliant, or just lucky? Probably a little bit of both. Or maybe the problem isn't so hard after all. But if it wasn't that hard, why did it take us 80,000 computer days? I just don't know, to be honest. In general, it's very hard to say whether a problem is hard or not. For some problems (or problem instances, to be precise), we have a few hallmarks that make them easy: small state-space, highly constrained, high solution density, availability of clues or good heuristics. But the absence of these ease-hallmarks still doesn't mean a problem is hard; it means we don't know. This problem has none of these hallmarks, or better: we haven't identified any. But since Resta's results and ours are so contradictory, we have absolutely no idea whether this problem is hard or easy. Maybe it depends on how lucky your are, or on where you look.

Left: solution found on the server of Cees van Leeuwen's [lab for perceptual dynamics] in Leuven. Thanks to Marco Maas for helping out too. Right: solution found on the astronomical supercomputer ASTRON in Dwingeloo, The Netherlands

Who are you guys?

We are a genuine VU-UvA consortium. Mark, Florian and Emiel were VU-students when we started this work. They're all professionals now, and Emiel does some occasional work in proofreading Heuristics-reports at the UvA. That's where I work, in the "minor programming" (www.mprog.nl) where we teach the course of Heuristics. That course was originally built up at the VU back when I worked there with Guszti Eiben and Bushra Malik. Sandjai, our senior author, also works at the VU as a Full Professor Business Analytics. He works on state-space reductions which is exactly the trick we deployed to solve ASQAS-34. So there's connections all over, we're truly a VU-UvA team.

Left-to-right: Mark Moes, Emiel Suilen & Florian Braam who did most of the ground work. Bottom right is me (Daan van den Berg), I did coordination and wrote the paper's first draft. Top right is Sandjai Bhulai who also did some writing and took care of the entire publication process. A good team.