MeesterDaan (talk | contribs) m |
MeesterDaan (talk | contribs) m |
||
| (11 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Inleiding== | ==Inleiding== | ||
| − | Er is de laatste jaren veel te doen omtrent datavisualisatie. het internet maakt grote hoevelheden gegevens publiekelijk opvraagbaar, maar zie er maar eens wijs uit te worden. De kunst van het goed in beeld brengen van data is daarom van essentieel belang | + | Er is de laatste jaren veel te doen omtrent datavisualisatie. het internet maakt grote hoevelheden gegevens publiekelijk opvraagbaar, maar zie er maar eens wijs uit te worden. De kunst van het goed in beeld brengen van data is daarom van essentieel belang. Deze opdracht is bedoeld om te kijken of we een redelijk kleuringsalgoritme kunnen vinden. Eerst eentje voor klassieke topografische kaarten, dan eentje voor ingewikkelder structuren van sociale netwerken. Homo digitalis factum est. |
| − | + | ==Opdracht 1== | |
| − | |||
| − | |||
| − | ==Opdracht== | ||
<Center> | <Center> | ||
{| align="center" | style=" align="center"; text-align: center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;" | {| align="center" | style=" align="center"; text-align: center; margin-left: 1em; margin-bottom: 1em; font-size: 100%;" | ||
| − | ! | + | !Kaart #1 |
| − | ! | + | !Kaart #2 |
| − | ! | + | !Kaart #3 |
|- | |- | ||
|valign="top" |[[Image:map1k.jpg|frame|link=file:map1.jpg|]] | |valign="top" |[[Image:map1k.jpg|frame|link=file:map1.jpg|]] | ||
| Line 25: | Line 22: | ||
</Center> | </Center> | ||
| − | a) Kies twee van de drie kaarten en kleur ze zo dat er zo min mogelijk kleuren nodig zijn. Het beste is om er een algoritme voor te schrijven, maar als je het liever met de hand doet kan dat ook, probeer dan wel alvast over het algoritme na te denken. | + | a) Kies twee van de drie kaarten en kleur ze zo dat er zo min mogelijk kleuren nodig zijn. Het beste is om er een algoritme voor te schrijven, maar als je het liever met de hand doet kan dat ook, probeer dan wel alvast over het algoritme na te denken. Als de derde kaart ook lukt, des te beter. |
| + | |||
b) Ontwerp een methode (algoritme) om kaarten te kleuren. Zorg dat je algoritme zo min mogelijk verschillende kleuren gebruikt, dit is goed voor de oogrust en ziet er professioneel uit. Denk allereerst na over hoe je een kaart in de computer moet representeren. | b) Ontwerp een methode (algoritme) om kaarten te kleuren. Zorg dat je algoritme zo min mogelijk verschillende kleuren gebruikt, dit is goed voor de oogrust en ziet er professioneel uit. Denk allereerst na over hoe je een kaart in de computer moet representeren. | ||
| − | |||
| − | + | ==Opdracht 2== | |
| + | |||
| + | Het marketingbedrijf Stalqingu4ever wil inzichtelijk hebben hoe ze facebook-, twitter en myspacegebruikers het best aan advertenties kunnen blootstellen. Ze willen daarom een kaart maken, waarop verbonden gebruikers verschillen van kleur. | ||
| + | |||
| + | c) Bijgaand is een [[http://heuristieken.nl/resources/NieuweSocialConnections_okt2015.xlsx bestand]] met daarin 3 netwerken van 100 geanonimiseerde gebruikers en hun connecties. Geef alle gebruikers een kleur zodat er zo min mogelijk kleuren gebruikt worden, terwijl verbonden gebruikers van kleur verschillen. Maak je kleuring op één of andere manier zichtbaar. | ||
==Advanced== | ==Advanced== | ||
| − | + | Kun je iets zeggen over de relatie tussen het aantal connecties en het minimum aantal kleuren dat je nodig hebt? Wees duidelijk met je argumenten, zeg niets dat je niet zeker weet. | |
| + | |||
==Links== | ==Links== | ||
| − | + | No links so far. | |
==Terug== | ==Terug== | ||
Terug naar de [[Heuristieken|Heuristieken hoofdpagina]]. | Terug naar de [[Heuristieken|Heuristieken hoofdpagina]]. | ||
Latest revision as of 11:17, 23 October 2015
Inleiding
Er is de laatste jaren veel te doen omtrent datavisualisatie. het internet maakt grote hoevelheden gegevens publiekelijk opvraagbaar, maar zie er maar eens wijs uit te worden. De kunst van het goed in beeld brengen van data is daarom van essentieel belang. Deze opdracht is bedoeld om te kijken of we een redelijk kleuringsalgoritme kunnen vinden. Eerst eentje voor klassieke topografische kaarten, dan eentje voor ingewikkelder structuren van sociale netwerken. Homo digitalis factum est.
Opdracht 1
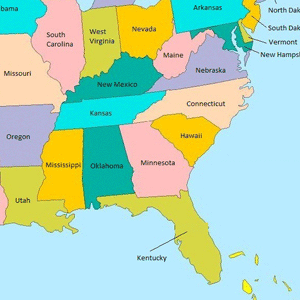
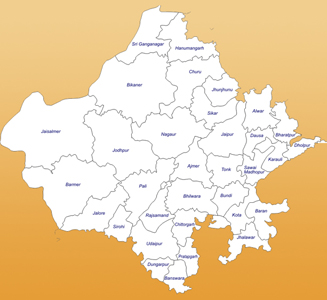
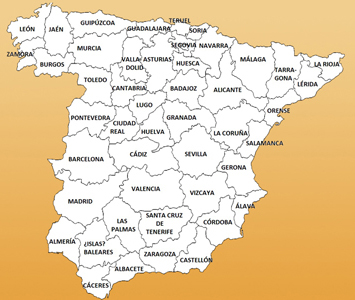
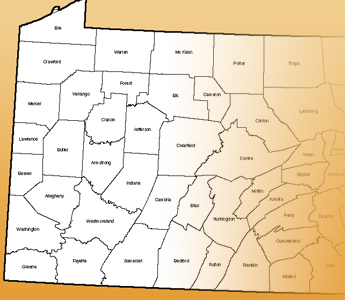
| Kaart #1 | Kaart #2 | Kaart #3 |
|---|---|---|
a) Kies twee van de drie kaarten en kleur ze zo dat er zo min mogelijk kleuren nodig zijn. Het beste is om er een algoritme voor te schrijven, maar als je het liever met de hand doet kan dat ook, probeer dan wel alvast over het algoritme na te denken. Als de derde kaart ook lukt, des te beter.
b) Ontwerp een methode (algoritme) om kaarten te kleuren. Zorg dat je algoritme zo min mogelijk verschillende kleuren gebruikt, dit is goed voor de oogrust en ziet er professioneel uit. Denk allereerst na over hoe je een kaart in de computer moet representeren.
Opdracht 2
Het marketingbedrijf Stalqingu4ever wil inzichtelijk hebben hoe ze facebook-, twitter en myspacegebruikers het best aan advertenties kunnen blootstellen. Ze willen daarom een kaart maken, waarop verbonden gebruikers verschillen van kleur.
c) Bijgaand is een [bestand] met daarin 3 netwerken van 100 geanonimiseerde gebruikers en hun connecties. Geef alle gebruikers een kleur zodat er zo min mogelijk kleuren gebruikt worden, terwijl verbonden gebruikers van kleur verschillen. Maak je kleuring op één of andere manier zichtbaar.
Advanced
Kun je iets zeggen over de relatie tussen het aantal connecties en het minimum aantal kleuren dat je nodig hebt? Wees duidelijk met je argumenten, zeg niets dat je niet zeker weet.
Links
No links so far.
Terug
Terug naar de Heuristieken hoofdpagina.