MeesterDaan (talk | contribs) m |
MeesterDaan (talk | contribs) (→Advanced) |
||
| Line 30: | Line 30: | ||
==Advanced== | ==Advanced== | ||
| − | We werken met rechthoeken waarvan de ene zijde net één eenheid korter is dan de andere zijde. | + | We werken met rechthoeken waarvan de ene zijde net één eenheid korter is dan de andere zijde. Tegelset #3 van de vorige opdracht bestaat uit rechthoeken 1 tot en met 20 (1x2, 2x3, 3x4 .... 20x21), die samen in een groter rechthoek (55x56) passen. Kijk of er een oplossing bestaat voor 1 tot en met 34. Je weet niet of de rechthoeken gedraaid moeten worden, en hoe groot het invoervlak moet zijn. Probeer het zo goed mogelijk te passen! |
| − | |||
==Links== | ==Links== | ||
Revision as of 13:41, 20 October 2015
Contents
Inleiding
Tegelzetten is een vak apart. Hoewel de meeste zettingen regelmatig zijn (denk aan de vierkantjes in keuken en badkamer) zijn er ook ambitieuzere patronen, zoals een Versailles-patroon waarin twee of drie verschillende tegeltjes in een veelal herhalend patroon worden gerangschikt. In een zeldzaam geval is de zetting echt onregelmatig, en is de kunstenaar of architect veel tijd kwijt aan het in elkaar puzzelen.
In deze opdracht zul je een algoritme ontwikkelen om tegelsets van oplopende moeilijkheid in elkaar te zetten.
Opdracht
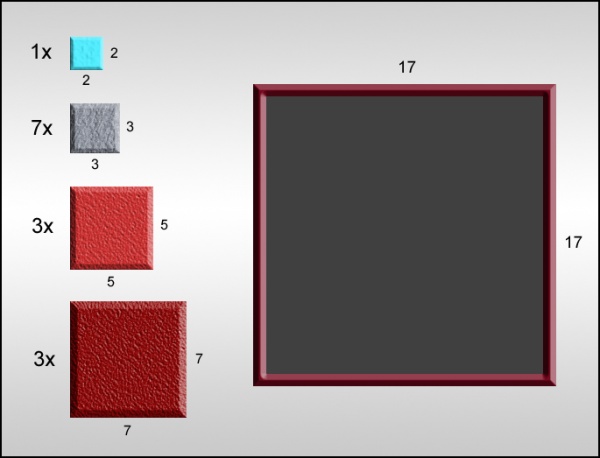
a) Verzin een algoritme om tegelset #1 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen.
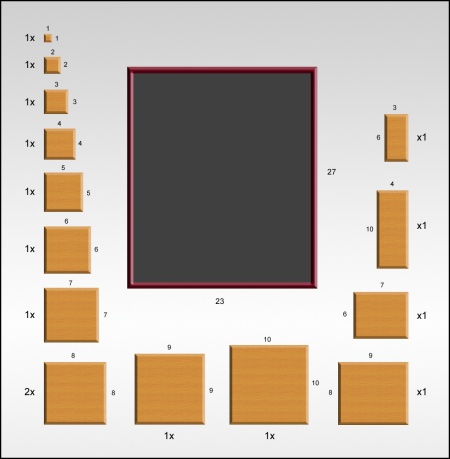
b) Verzin een algoritme om tegelset #2 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen. Tegels hoeven niet gedraaid te worden.
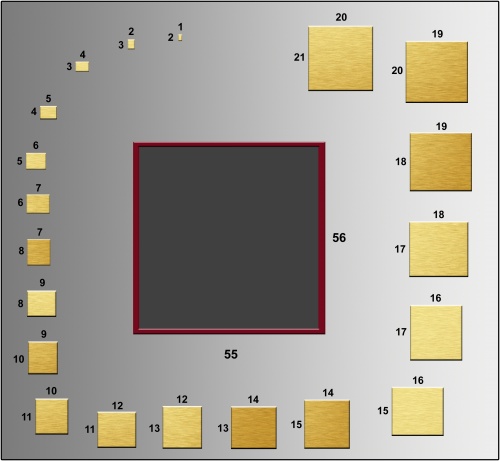
c) Verzin een algoritme om tegelset #3 in het bijgeleverde invoervak te zetten. Een zetting is correct als er geen tussenruimte tussen de tegels is, en tegels elkaar niet overlappen.
d) Er zijn nieuwe tegelsets beschikbaar gemaakt door onze collega's van de VU, maar zijn ze eigenlijk wel oplosbaar?
Advanced
We werken met rechthoeken waarvan de ene zijde net één eenheid korter is dan de andere zijde. Tegelset #3 van de vorige opdracht bestaat uit rechthoeken 1 tot en met 20 (1x2, 2x3, 3x4 .... 20x21), die samen in een groter rechthoek (55x56) passen. Kijk of er een oplossing bestaat voor 1 tot en met 34. Je weet niet of de rechthoeken gedraaid moeten worden, en hoe groot het invoervlak moet zijn. Probeer het zo goed mogelijk te passen!
Links
Best leuk om even te kijken naar perfect squares op WolframMathWorld.
Terug
Terug naar de Heuristieken hoofdpagina.