Chips & Circuits

Introduction

Chips (or more precisely: integrated circuits) are found in your PC, MacBook, Android Phone and microwave oven where they perform a diversity of frunctions, ranging from timekeeping and motor control to arithmetical calculations. Basically a small plate of silicon supporting a considerable number of connected logical gates, chips are usually designed by a logical design, subsequentially transformed to a list of connectable logical gates (commonly known as a net list) and in the final step transformed to 2-dimensional design on a silicon base.

This last step however, the physical real-world process of connecting the gates, is highly volatile. Good arrangements on the base lead to short connections, leading to faster circuits, whereas poor arrangements lead to slower circuits. It leads to no doubt that a good arrangement of logical gates is of vital essence to the value of the IC as a whole.

Example #1

Given netlist#1, connecting five logical gates on a grid. Gates cannot be on directly adjacent grid points because of the produced heat. They should be connected in exact correspondence to the netlist, though connections can be considered to be undirected for the scope of this case. Gates to not have an in- or output side; connections can enter or exit at any point from a gate. Connections must follow grid lines for reasons of manufacture, but connections between different gates cannot cross.

Netlist #1:
A	B,C;
C	E;
D	B;
E	C,D

thumb Game #2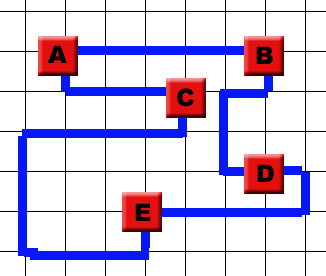

As can be seen, even for this one very simple netrlist, a great variety can be achieved in terms of optimality. The left picture has substantially shorter wires (total wire length: 92), resulting in a much faster processor than the right picture (total wire length: 124) which is functionally identical, but a lot slower.

Assignment

1) Write an algorithm that calculates the total wire length of any given placement of logical gates on a grid.

2) Write an algorithm that takes a netlist as input. It should check whether the wires cross, and if they do, return an error message. If the wires do not cross, it should place the gates on a grid and calculate the total wire length. It does not need to be optimal.

3) Test your algorithm on netlist #2.

4) Improve your algorithm such, that it minimizes the wire length for netlist#2. This might be quite hard.

Advanced

The suspicion is, that the minimal number of layers required for a chip to be designed from a netlist depends on the connectivity of the netlist. Generate 10 random netlists with the exact same number of gates and connections as in netlist#3 and run them through your algorithm. Carefully document the number of layers needed and the optimality of the found solution. Next, double the number of connections for each netlist and run them through your algorithm again. Document carefully again, and compare the results with the previous experiment.

Links

Nothing here for now.

Go Back

Go back to the Heuristics Main Page.